本文主要介绍单相半桥逆变电路和单相全桥逆变电路,分别对工作模态进行了简要分析;同时介绍了移相调压和脉宽调制两种控制方式,其中脉宽调制是更常用的控制方式。在文末也附上了仿真电路资源。
1 逆变电路基本原理
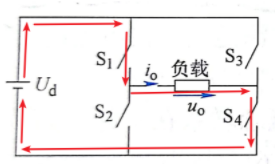
模态一
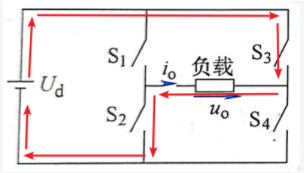
模态二
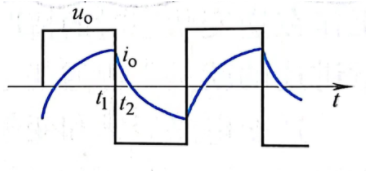
模态三
如上图所示,是单相桥式逆变电路的在纯阻性负载下的简化电路
其工作模态是:
模态一: 0-t_1时 T_1、T_4闭合,负载电压为 +V_d
模态二: t_1-T时 T_2、T_3闭合,负载电压为 -V_d
纯阻性负载下电压电流是同相位的,如果是感性负载,那么电流波形会滞后于电压的波形,并且因为负载电感的存在,负载电流的变化也不是瞬态的,而是会有上升、下降的过程的。而最终现象是电流变化总是比电压变化慢的。
2 半桥逆变电路(Half-Bridge Inverter Circuit)
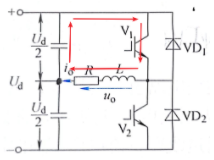
模态一
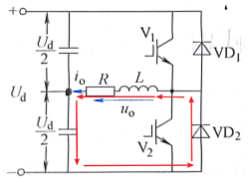
模态二
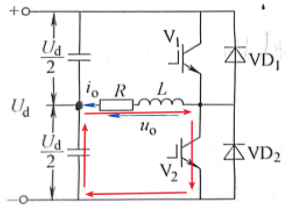
模态三
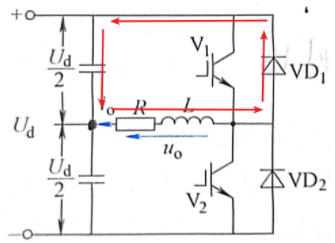
模态四
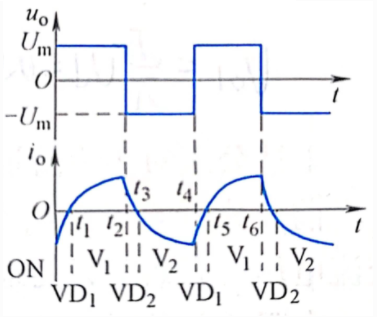
半桥逆变电压电流(移相调压)
半桥逆变电路拓扑是其他逆变电路的基础,因此可以理解为半桥逆变电路的工作原理是很必要的,那么如上图即为半桥逆变电路的工作模态 ( U_m=\frac{1}{2}U_d):
模态分析
模态一: t_1-t_2时, V_1闭合、 V_2断开,由直流源供电,电感储能,电流增大;
模态二: t_2-t_3时, V_1断开、 V_2闭合,由于 感性负载电流方向不能突变,所以 VD_2续流,由电感为负载供能,电流迅速减小;
模态三: t_3-t_4时,电感电流减小至零后 V_2闭合,电感电流反向流过 V_2;
模态四: t_4-t_5时, V_1闭合、 V_2断开,同理 V_1不能马上闭合, VD_1续流,电流迅速减小;
当 V_1或 V_2闭合时,负载电流和电压同向,直流侧给交流侧提供能量;当 VD_1或 VD_2闭合时,负载电流和电压反向,负载电感中存储的能量向直流侧反馈,即负载电感将其吸收的无功能量向直流侧反馈,其反馈的能量暂时存储在直流侧电容中(直流侧电容具有缓冲这种反馈回来的无功能量的作用)。
因为 VD_1和 VD_2是无功功率反馈回直流侧的通道,所以称为“反馈二极管”;又因为起着使负载电流连续的作用,所以又称为“续流二极管”。
3 全桥逆变电路(Full-Bridge Inverter Circuit)
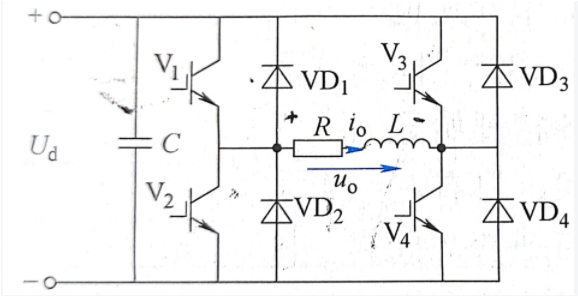
全桥逆变拓扑结构图

电压电流波形图(负载类型和半桥逆变相同)
上图即为全桥逆变电路(U_m=U_d),它可以看成由两个半桥电路组成(在直流电压 U_d和负载都相同的情况下,其输出电流 i_o 的波形也就和半桥逆变波形相同,只有幅值会增加一倍)。把桥臂1和4作为一对,桥臂2和3作为一对,成对的两个桥臂同时导通,两对交替各导通180°。无功能量的转换也是同理的。
对全桥逆变输出电压波形做定量分析,把幅值为 U_d的矩形波 u_o展开成傅里叶级数得:
其中基波的幅值 U_{o1m}和基波有效值 U_{o1}分别为:
上述定量分析同样适用于半桥逆变电路:
以上分析都是 u_o为正负电压各位180°的脉冲时的情况,在这种情况下,要改变输出交流电压的有效值只能通过改变直流电压 U_d来实现。(关系式如上所示)
3.1 全桥逆变-移相调压
当负载为阻感负载时,还可以通过移相的方式来调节逆变电路的输出电压,称为移相调压。移相调压实际上是调节输出电压的脉宽,如下图中的电压电流波形图中, V_1和 V_2互补, V_3和 V_4互补,但是 V_3不是比 V_1落后180°,而是只落后 \theta(0<\theta <180°)。如此一来输出电压 u_o就不再是正负各为180°的脉冲,而是正负各为 \theta的脉冲。
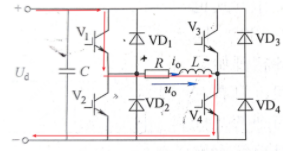
模态一
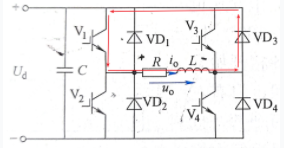
模态二
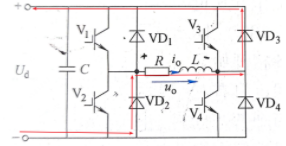
模态三
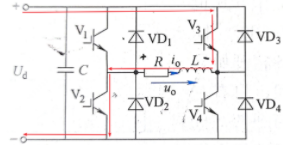
模态四
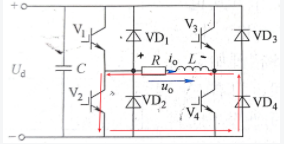
模态五
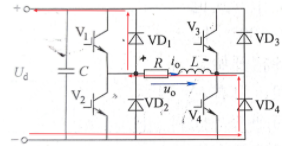
模态六
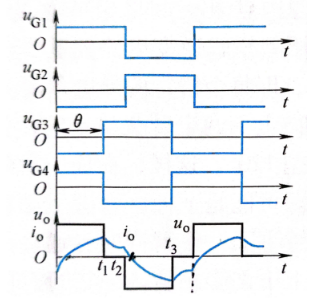
全桥逆变电压电流(移相调压)
模态分析
模态一:假设在 t_1时刻前, V_1和 V_4导通,输出电压 u_o=U_d;
模态二: t_1时刻 V_3和 V_4驱动信号反向, V_4截止,因为负载电感中电流 i_o不能突变, V_3不能立刻导通, VD_3导通续流。因为 V_1和 VD_3同时导通,所以输出电压 u_o=U_d;
模态三: t_2时刻 V_1和 V_2驱动信号反向, V_1截止,同理 V_2不能立刻导通, VD_2导通续流,和 VD_3构成回路,输出电压 u_o=-U_d;
模态四:负载电流过零点并开始反向时, VD_2和 VD_3截止, V_2和 V_3开始导通,输出电压仍为 u_o=-U_d;
模态五: t_3时刻 V_3和 V_4驱动信号反向, V_3截止,同理 V_4不能立即导通, VD_4续流,输出电压 u_o=0;
模态六: t_4时刻, V_1和 V_2驱动信号反向, V_2截止, V_1不能立即导通, VD_1导通续流,和 VD_4构成回路,输出电压 u_o=U_d。
电路仿真
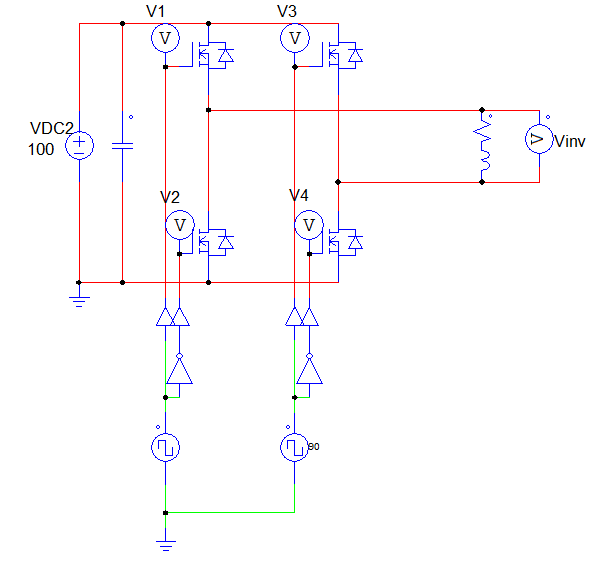
全桥逆变电路仿真图(移相调压)
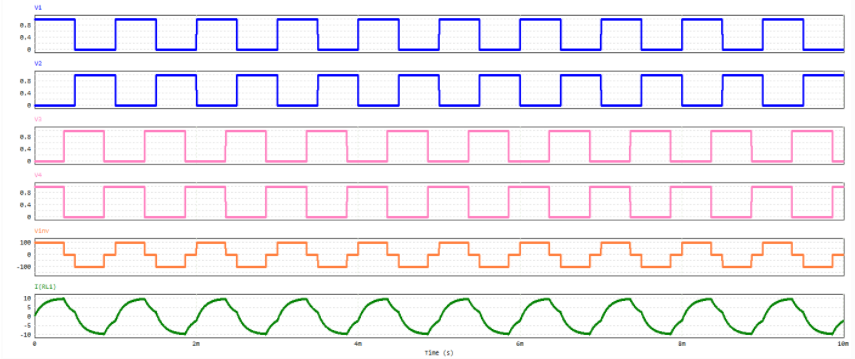
全桥逆变电路电压、电流、驱动信号波形图(移相调压)
3.2 全桥逆变-脉宽调制
根据采样控制理论中的结论:面积(冲量)相等而形状窄脉冲加在惯性环节上时,其效果基本相同。是PWM可控制技术的重要理论基础。
将正弦波看成是由N个彼此相连的脉冲序列组成的波形,如下图b所示,各脉冲幅值相等而脉冲的宽度按照正弦规律变化,根据面积等效原理,PWM波形和正弦波是等效的。对于正弦波的负半周期同样如此。像这种脉宽按正弦规律变化和正弦波等效的PWM波形也称为SPWM波。要改变等效输出正弦波的复制时,只要按照同一比例系数改变脉宽即可。
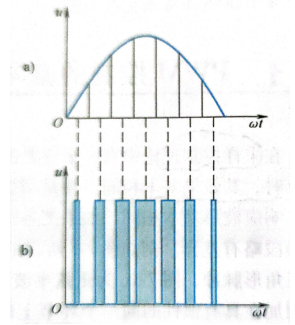
PWM等效正弦半波(负半周期同理)
根据上述PWM控制的基本原理,如果已知逆变电路的正弦波输出频率(如50HZ/60Hz),幅值(220V/110V)以及半波周期内的脉冲数(即方波脉冲个数),那么PWM波形中各脉宽以及间隔均可准确计算,根据计算结果控制电路中开关器件的通断,就可以得到预期的PWM波,这种方法称为计算法(不常用,因为因素太多导致计算相当繁琐)。
另外就是调制法,即把期望输出的波形作为调制波,把接受调制的信号作为载波,通过调制就可以得到预期的PWM波。通常采用等腰三角形波或锯齿波作为载波(任意一点的水平宽度和高度成线性关系,当它与任何一个平缓变化的调制波相交时,在交点时刻对开关器件进行通断控制,就可以得到宽度正比于幅值的脉冲,而往往前者由于具有对称性实际应用更为广泛)。当调制信号为正弦波时,得到的便是SPWM波。如下图所示:
图中 u_c为载波、 u_r为调制波(正弦波)、 u_o为输出的SPWM电压波形、 u_{of}为 u_o的基波分量。
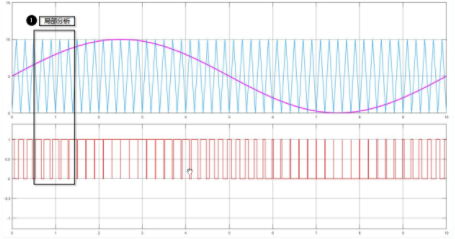
SPWM波形
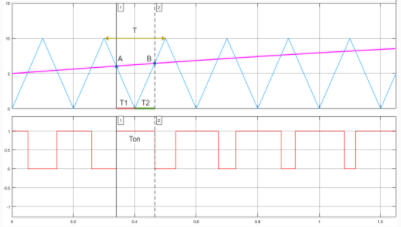
波形细节
结合拓扑电路进行分析:
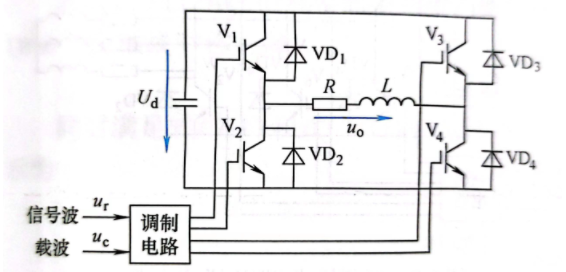
全桥逆变电路(PWM控制)
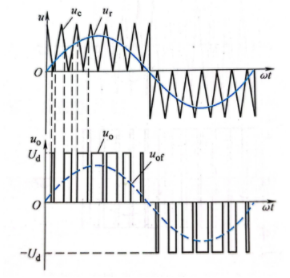
单极性PWM控制方式波形
假设负载为阻感负载,工作时 V_1和 V_2通断状态互补, V_3和 V_4通断状态互补。
3.2.1 单极性调制
控制 V_3和 V_4的方法如单极性PWM控制方式波形图所示:调制波 u_r为正弦波,载波 u_c在 u_r正半周期时为正极性的三角波,正在 u_r的负半周期为负极性的三角波。在 u_r和 u_c的交点时刻控制开关的通断,在 u_r的正半周, V_1保持导通, V_2保持关断,当 u_r>u_c时使 V_4导通, V_3关断, u_o=U_d;当 u_r<u_c时使 V_4关断, V_3导通, u_o=0。在 u_r的负半周期, V_1保持关断, V_2保持导通,当 u_r<u_c时使 V_3导通, V_4关断, u_o=-U_d;当 u_r>u_c时使 V_3关断, V_4导通, u_o=0。如此一来便可以得到SPWM波形 u_o。像这样在 u_r半个周期内三角波只在正极性或负极性一种极性范围内变化,所得到的PWM波形也是在单个极性范围变化的控制方式即为单极性调制方式。
单极性调制模态分析
电压正半周期: V_1保持导通, V_2保持关断, V_3和 V_4交替导通和关断。由于负载电流比电压滞后,所以在电压 u_o的正半周,电流有一段为正,有一段为负。如下图所示(图中框出来的分别是输出电压正半周期电流负值阶段,输出电压负半周期时电流正半周期阶段):

输出电压电流波形
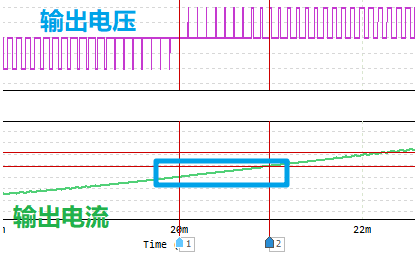
输出电压正半周期,输出电流为负值阶段
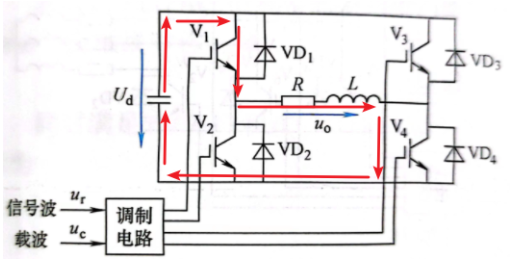
模态一
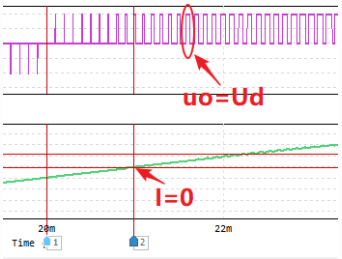
模态一波形图
模态一:在负载电流为正的区间里, V_1和 V_4导通时,负载电压 u_o等于直流电压 U_d;
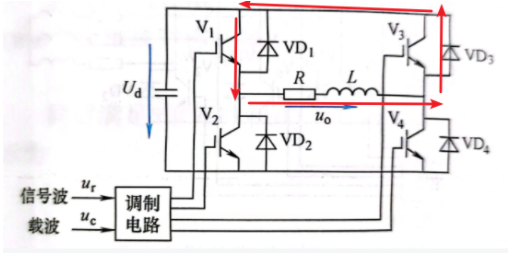
模态二
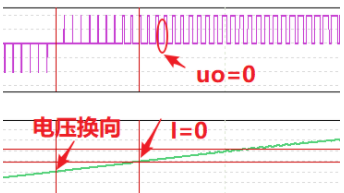
模态二波形图
模态二:在负载电流为正的区间里, V_1导通而 V_4关断时,负载电流通过 V_1和 VD_3续流, u_o=0;
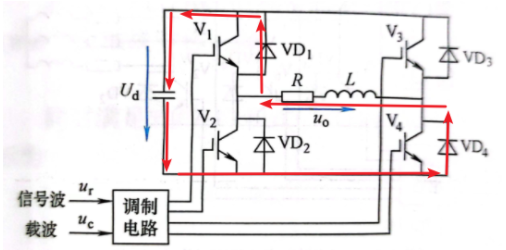
模态三
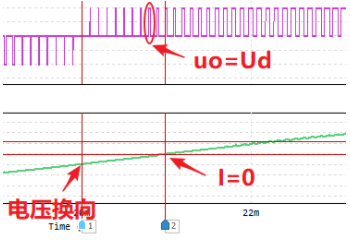
模态三波形图
模态三:在负载电流为负的区间里,仍然当 V_1和 V_4导通时,因为此时电流 I_o小于零,所以 i_o实际上是从 VD_1和 VD_4续流而过,仍有 u_o=U_d;
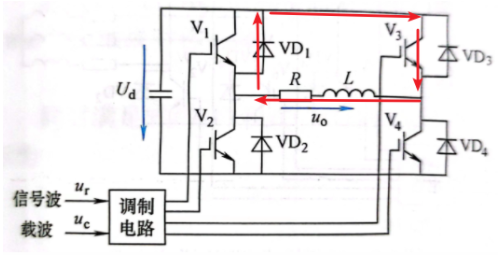
模态四
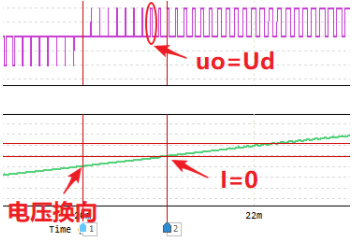
模态四波形图
模态四:在负载电流为负的区间里,当 V_4关断, V_3导通后, i_o从 V_3和 VD_1续流,此时 u_o=0。
电压负半周期: V_1保持关断, V_2保持导通, V_3和 V_4交替导通和关断。模态和正半周期同理可推。
电路仿真
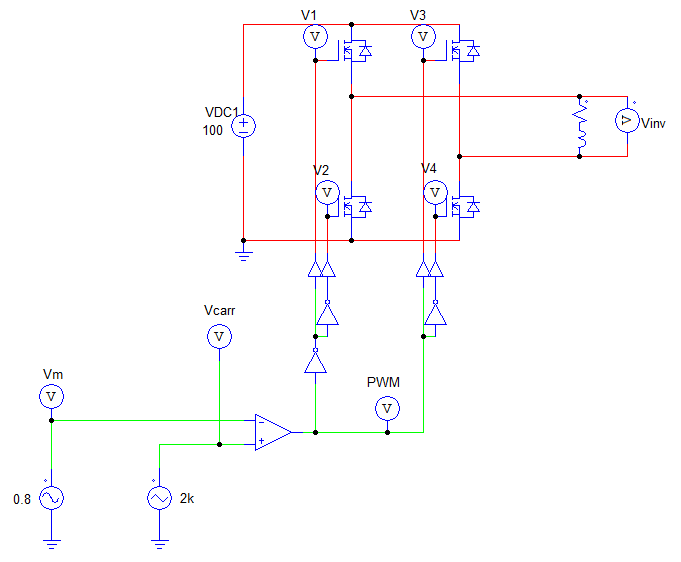
全桥逆变单极性PWM调制仿真电路
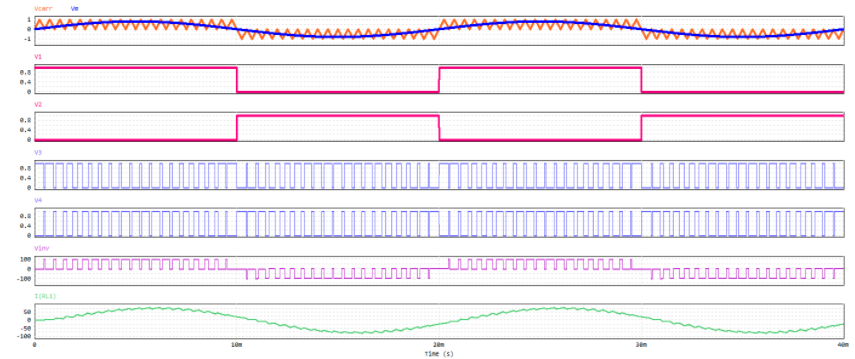
全桥逆变单极性PWM调制仿真波形
3.2.2 双极性调制
双极性调制,在 u_r的半个周期内,三角波载波不再是单极性的,而是有正有负的,所得的PWM波也是有正有负。在 u_r的一个周期内,输出的PWM波只有 ±U_d两种电平,而不再像单极性控制时还有零电平。仍然在调制波 u_r和载波 u_c的交点时刻控制开关器件的通断。在 u_r的正负半周,对各开关器件的控制规律相同。
当 u_r>u_c时,给 V_1和 V_4导通信号,给 V_2的 V_3关断信号,此时如果 i_o>0则 V_1和 V_4导通,如果 i_o<0则 VD_1和 VD_4导通续流,这两种情况的输出电压 u_o=U_d;当 u_r<u_c时, V_2和 V_3导通, V_1和 V_4关断,此时如果 i_o<0,则 V_2和 V_3导通,如果 i_o>0,则 VD_2和 VD_3单通,这两种情况的输出电压都是 u_o=-U_d。
具体模态不再分析,可以根据仿真波形具体分析,相比单极性,双极性更好分析。

全桥逆变双极性PWM调制仿真电路
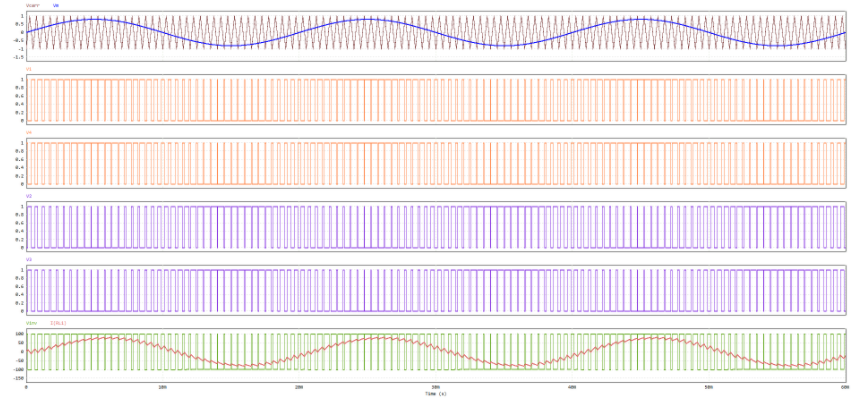
全桥逆变双极性PWM调制仿真波形
参考文献
[1]电力电子技术第五版 王兆安


评论区