ADC(Analog to Digital Converter)顾名思义,实现将模拟信号转换为数字信号,而ADC采样过程包含四个阶段,即:抗混叠滤波(Anti-aliasing)、采样保持电路(Sample and Hold)、量化(Quantizer)、编码(Coder)。
1 初始ADC
1.1 ADC采样过程
抗混叠滤波:理解为对ADC IP的输入信号进行低通滤波的环节;
采样保持电路:又称“采保电路”,将连续的模拟量转换为离散的模拟量的过程称为采样,将转换得到的结果保持到下一次采样开始的过程称为保持;
量化和编码:使用N位二进制数度量模拟量的过程称为量化,将模拟量所对应的二进制数值编译成数值的过程称为编码。
Example 1:
一个N位的ADC,其满量程电压为 V_{ref},划分为 2^N个等间隔区间,区间宽度用LSB(Last Significant Bit|最低有效位), LSB=\frac{V_{ref}}{2^N}。
例如: V_{ref}=8V,ADC为3bit,LSB=1,所以每个区间表示1V
000代表电压 0\leq V_{real}<1;001代表电压 1\leq V_{real}<2 ... 111代表电压 7\leq V_{real}<8。
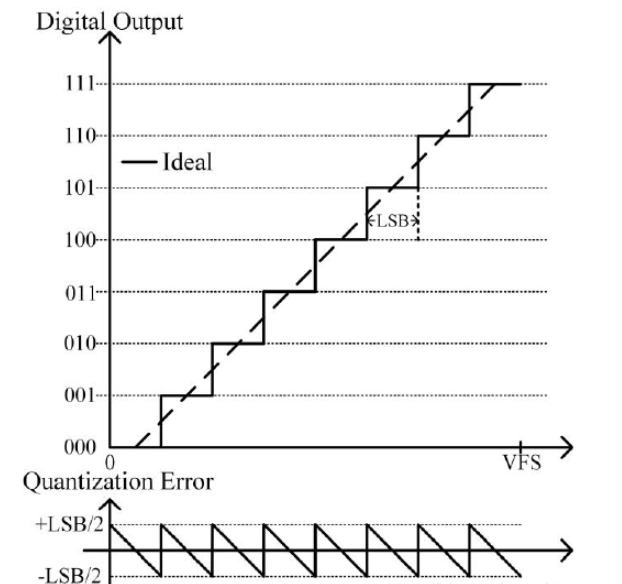
数字信号输出和量化误差
1.2 ADC分类
ADC主要分为逐次逼近型,双积分型ADC以及Sigma-Delta ADC,其中逐次比较型ADC应用范围最为广泛,Sigma-Delat ADC随着发展以及某些领域对于精度的需求,应用也开始普遍起来(会有专门的篇章讨论Sigma-Detal ADC)。
1.2.1 逐次逼近型(Successive Approximation Register)
其原理是从高位到地位逐位试探比较,类似与使用天平从中到轻逐级递减砝码进行试探。
逐次逼近型的转换过程是:初始化所有ADC,寄存器所有位全部清零;转换开始时先将逐次逼近寄存器最高位置1,送入D/A转换器,经D/A转换后生成的模拟量 V_{dac}送入比较器与待转换的模拟量 V_i进行比较,若 V_{dac}<V_i该位1被保留,否则清除。然后在置逐次逼近寄存器次高位为1,将寄存器中新的数字量送入D/A转换器,输出的 V_o再与输入 V_i比较(直到比较完成 V_i都不会变),若 V_o<V_i,该位被保留,否则清楚。重复该过程,直至逼近寄存器最低位。转换结束后,将逐次逼近寄存器中的数字量送入结果寄存器,得到数字量输出。
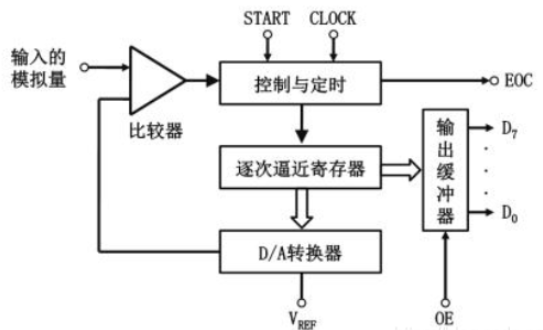
逐次比较型ADC原理框图
1.2.2 双积分型
其原理是将输入电压变换成与其平均值成正比的时间间隔,再把时间间隔转换成数字量,属于间接转换。转换过程是:开关导通, V_i输入到积分器,积分器从零开始固定时间T正向积分,时间T到后,开关再接通与 V_i极性相反的基准电压 V_{ref},将基准电压输入到积分器进行反向积分,直到输出位0V时停止积分。 V_i越大,积分器输出电压越大,反向积分时间也越长。计数器在反向积分时间内所计的数值就是 V_i的数字量,实现了A/D转换。
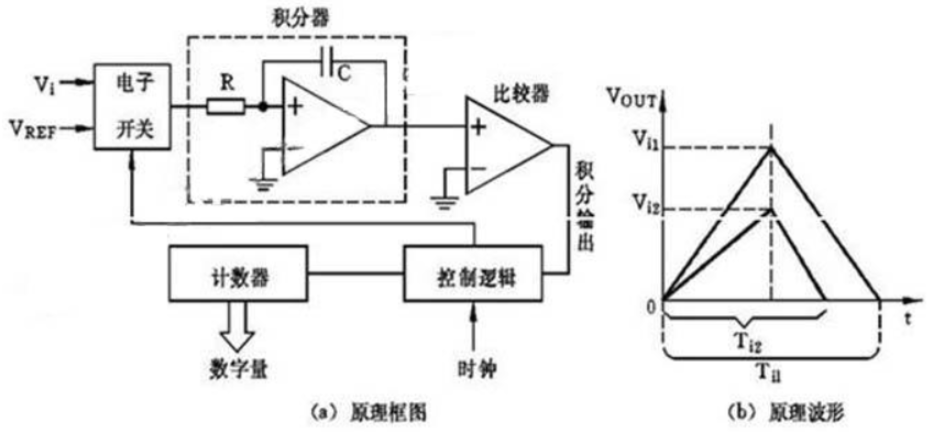
双积分型ADC原理框图
1.3 ADC参数
1.3.1 基本参数
分辨率:数字量变化一个最小单位时模拟信号的变化量,定义为满刻度与2^N的比值,通常以数字信号的位数来表示,位数越多,转换的精度越高,分辨率也就越高,但是ADC的精度不仅仅取决于分辨率;
转换速率:指A/D转换一次所需要时间(因为一个模拟信号转换成一个数字量不能瞬间完成,这个过程需要一定时间)的倒数,即单位时间内完成A/D转换的次数;
采样速率:采样速率是为最高的ADC采样频率,通常手册中描述为Maximum Sampling Frequency,为了保证转换完成,一般采样速率必须小于等于转换速率,即采样时间大于等于转换时间;
量程:允许输入得模拟信号范围;
最低有效位:又称为最小分辨率,LSB,满量程值以ADC分辨率的比值即为LSB,如一个4位ADC,数字量最高可以表示 2^4=16,满量程5V,那么最小的分辨率为 \frac{5V}{16}=0.31V,也就是说这个ADC可以分辨的最小电压时0.31V,可以用0001表示0.31V这个模拟量。LSB越小表明ADC精度越高。
1.3.2 静态参数
微分非线性(Differential Nonlinearity,DNL):简单的来说DNL特性就是,理论上我们用数字量的台阶去给模拟电压值进行编码的时候,台阶的宽度应该都是一样的,也就是说当ADC输入和输出成线性关系的时候,每次模拟输入按照LSB步进的时候,数字输出的增加1,也就是0000变成0001的过程。但是由于DNL,导致可能当数字输出由1000变为1001的时候,模拟的值变化却不是按照LSB进行增长,可能多一点也可能少一点,如下图所示:
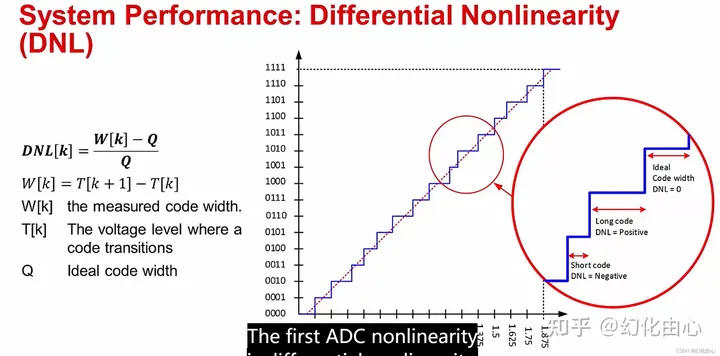
微分非线性阶梯图
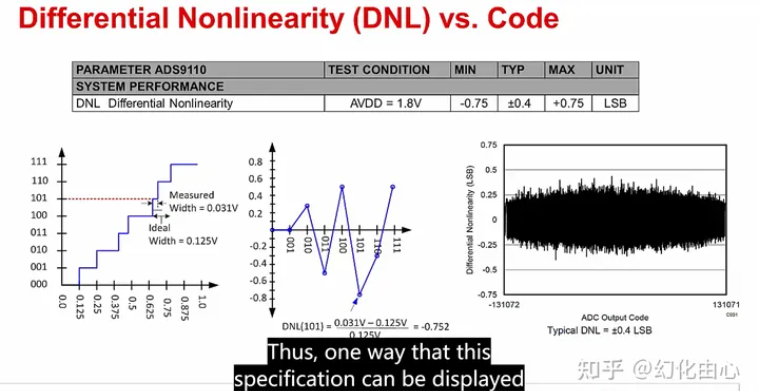
微分非线性阶梯图
根据DNL的特性,在最坏的情况下某一时刻由于DNL误差导致正向多了0.5LSB,下一时刻负向少了0.5LSB,可能会导致编码时丢码,如下图所示:
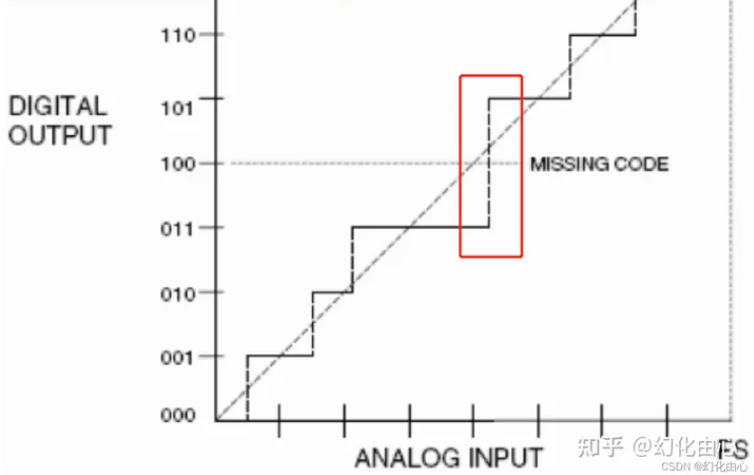
丢码现象图
很多的ADC都会有NMC参数(No Missing Codes)即为不丢码的范围,保证不会出现的DNL丢码这种极限情况。
积分非线性(Integral Nonlinearity,INL):积分大多数和累积误差相关,根据实际的模拟出一条曲线。INL是指ADC器件在所有的数值点上对应的模拟值和真实值之间误差最大的那点的误差值,表示测量值的绝对误差。下图绿色虚线为理想曲线方法(两点法)。红色虚线根据实际情况模拟出的曲线,找到两条曲线纵坐标差距最大的点。
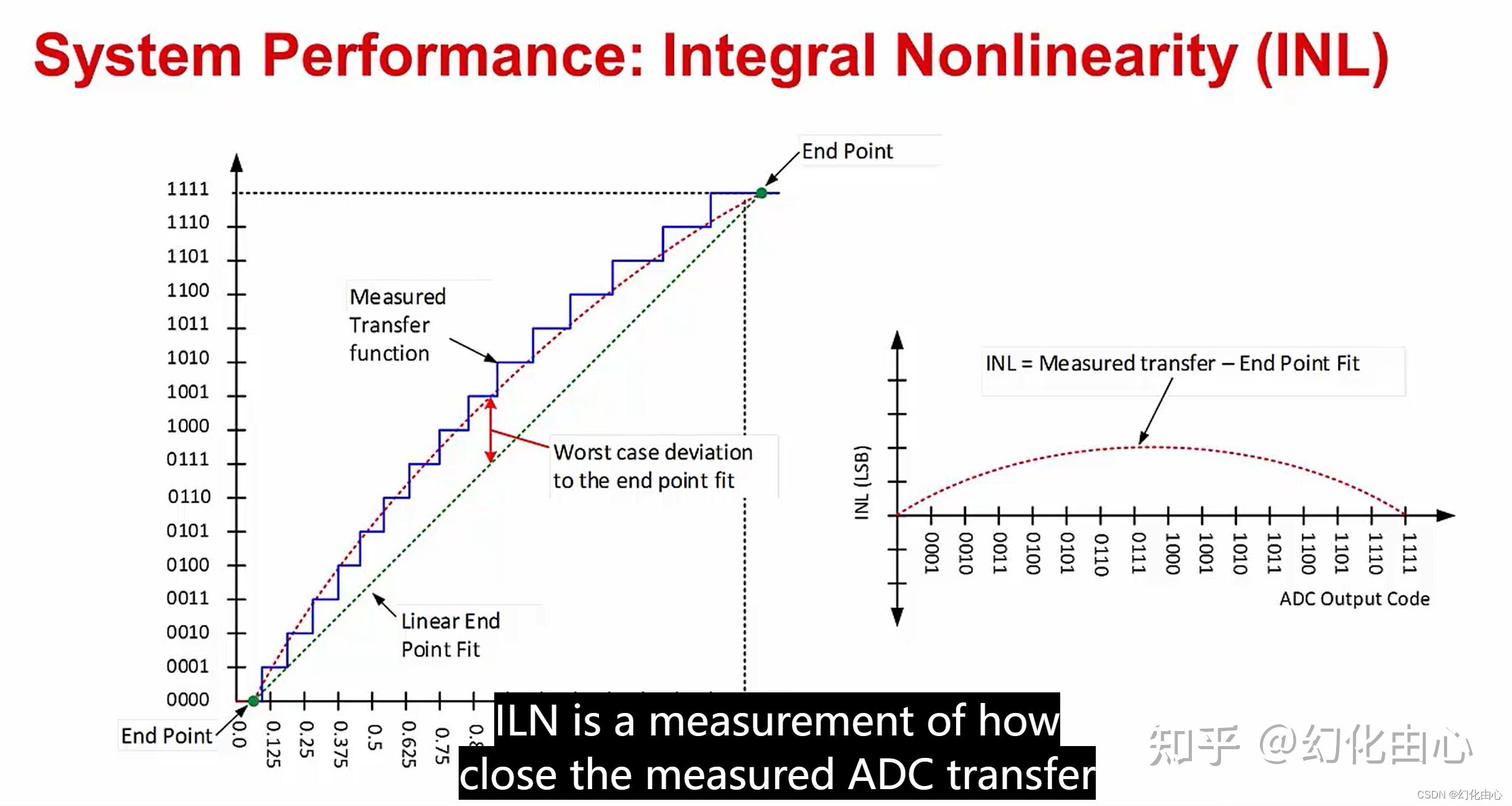
积分非线性阶梯图
可以用ppm来表征,也可以用LSB。

表征单位
INL和ADC累积的误差有关,DNL和ADC单次步进的误差有关,正好对应了微分(瞬时)和积分(累积)的特点。
1.3.3 动态参数
信纳比(SINAD): 信纳比=\frac{信号功率+噪声功率+谐波功率}{噪声功率+谐波功率}=SINAD=\frac{S+N+D}{N+D},即所有信号功率与所有非输出信号功率之比。SINAD可以反应ADC的整体动态性能,因为它包括所有构成的噪声和失真成分。
信噪比(SNR):为信号与噪声的比值 SNR=20log_{10}[\frac{V_{FS RMS}}{V_{NOISE RMS}}],理想状态下只考虑ADC的量化噪声,即可推出SNR理想值。(具体推导过程参考ADC过采样原理 - 白日梦想家)
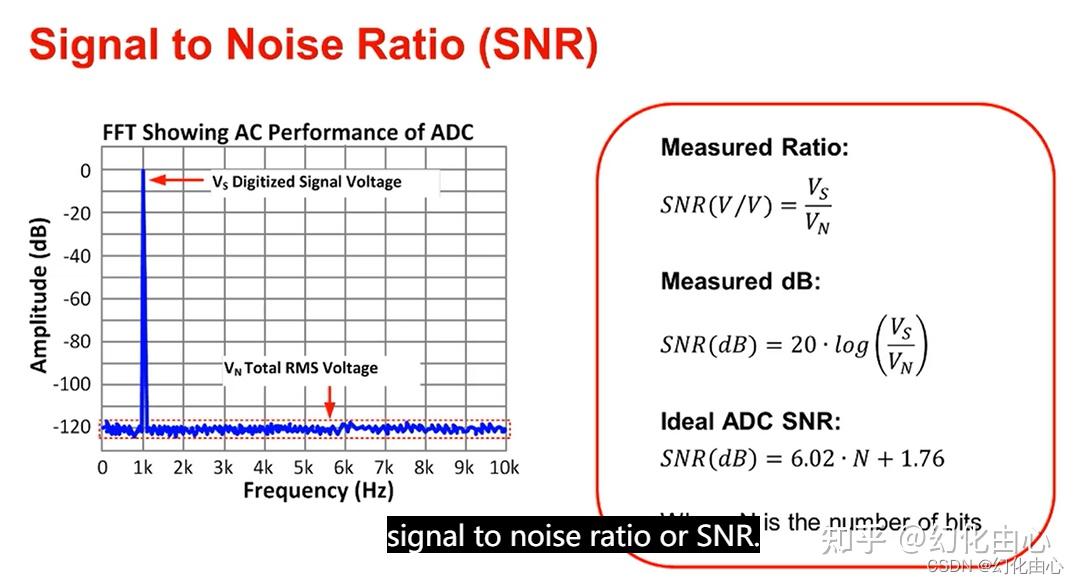
信噪比
有效位数(ENOB):有效位数和有效分辨率不能混为一谈,ENOB包括了量化噪声和失真项,有效分辨率用来衡量ADC在无量化噪声的直流输入条件下的噪声。将计算所得的SINAD值替换SNR,并求解ENOB,即: ENOB=\frac{SINAD-1.76dB}{6.02}
总谐波失真(Total Harmonic Distirtion,THD):输入信号与系统所有谐波的总功率之比。输出信号比输入信号多出的谐波成分。谐波失真是系统不完全线性造成的。所有附加谐波之和称为总谐波失真。总谐波失真与频率有关。一般1KHz处的总谐波失真最小,ADC输出中的谐波失真是由ADC特性中任何非线性引起的。每个ADC都具有非线性特性,也就是说每个ADC的输出都会存在谐波。DNL和INL是ADC非线性特性的度量,而THD是ADC输出产生的谐波失真的度量。
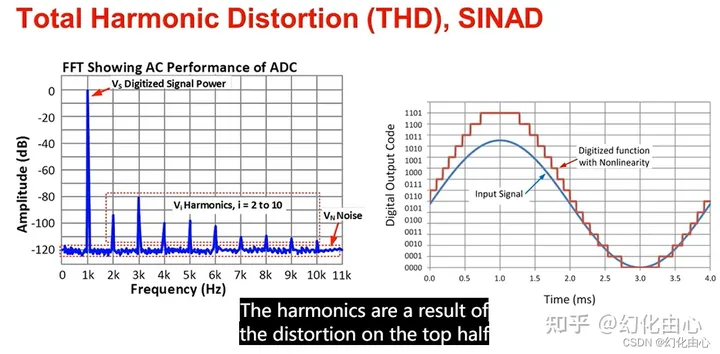
无杂散动态范围(Spurious-Free Dynamic range,SFDR):反应了FFT分析频谱中信号幅值与最大谐波的距离关系。所以SFDR值越大则说明系统的噪声水平越低,ADC的动态性能越好。单位dBc相对于载波频率幅度,dBFS相对ADC满量程范围。
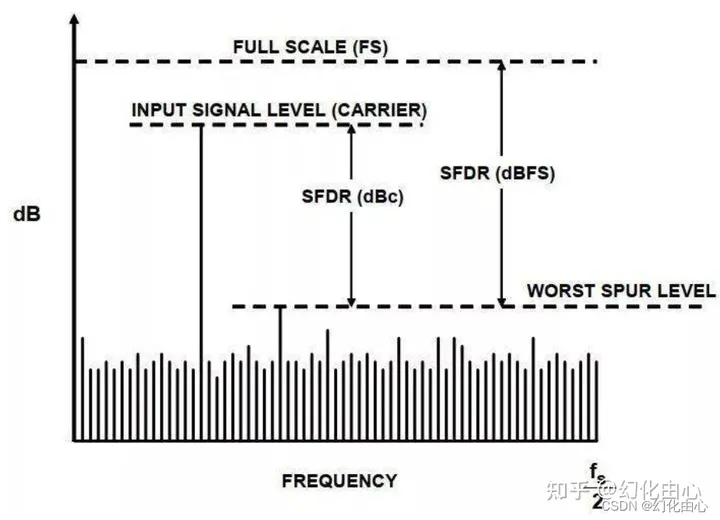
对于高速ADC,若要最大程度地提升SFDR,存在两个基本限制:首先是 前端放大器和采样保持电路产生失真;其次是 ADC编码器实际传递的非线性导致的失真。提高SFDR的关键是尽可能降低以上两种非线性。
2 ADC模式及其应用
ADC的工作模式可参见下面两篇文档:


评论区