使用ADC时,解决由于IP本身限制或者精度不够而无法满足应用上的需求,从而提高ADC位数的技术——过采样。ADC的过采样可以由软件、硬件实现。本文主要分析过采样实现的基本原理,围绕STM32的三种过采样方式展开分析,分别为利用白噪声实现过采样、使用三角抖动方法实现过采样、硬件过采样,主要分析第一种过采样方式。
过采样技术
过采样是一种提高信号采集质量的方法,而采集质量往往会被很多因素所干扰,比如环境的噪声过大对采样值亦有可能产生影响,但通常我们考虑的是IP本身可能会带来影响,例如在认识ADC - 白日梦想家中就有提到过量化误差一概念,在ADC将模拟信号转换为数字信号时,数字信号表征的数值与模拟信号实际值之间的误差称为 量化误差。量化的分辨率取决于二进制输出字长,通常为6~18bit的范围内。在对信号进行数字化时,理想转换器的最大误差为 \pm 1/2LSB(最低有效位)。
LSB通常被称为量子q,假设一个N位ADC和满量程电压$V_{AREF}$,量子q为两个相邻ADC码之间的最小距离。
锯齿波信号可以很好的表征量化误差,类似于宽带噪声。
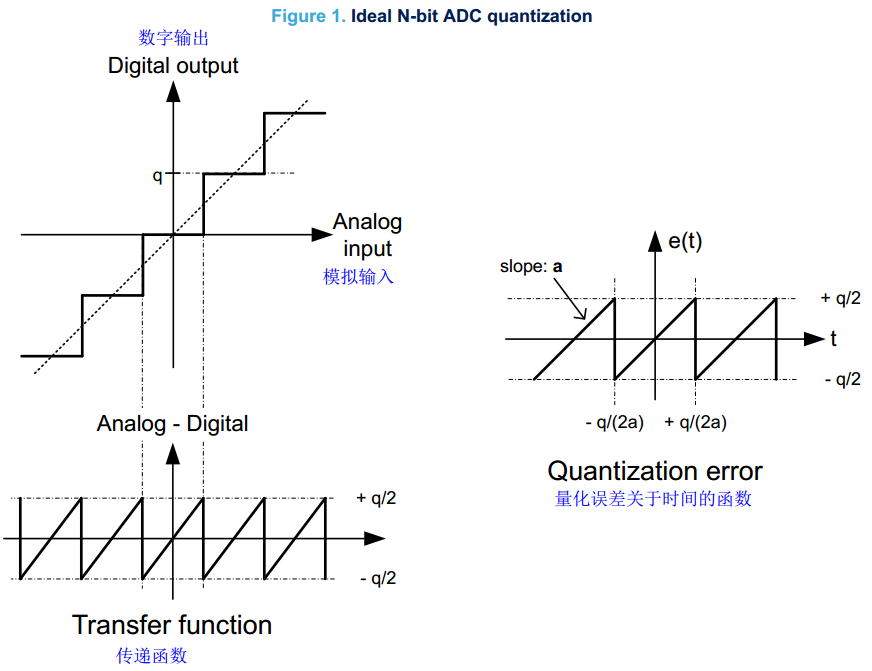
量化误差的定义式为:
量化误差的均方根为:
理想ADC的SNR是ADC噪声与输入信号功率的比值,假设信噪比等于量化噪声与输入信号的比值,不考虑其他噪声源。对于满量程的正弦波来说:
所以理想的N位ADC信噪比为:
其中RMS量化噪声是在整个奈奎斯特带宽测量得到的
当有效位数N增大时,信噪比增加6.02dB,对于实际ADC应用,必须要考虑不同的误差源:偏移、INL、DNL等,而这些描述在MCU数据手册中有。这些误差降低了ADC的理想分辨率,并决定了ADC真实的有效位数(ENOB)。提高信噪比可以提高ADC的有效位数。
奈奎斯特定理指出,为了重建模拟输入信号,必须以大于输入信号最大频率分量两倍的速率(采样频率)对信号进行采样。如果不符合奈奎斯特定理,模拟信号就不能从输入样本中恢复。所以对于大多数的应用,ADC输入端需要用一个低通滤波器过滤低于采样频率一半的频率。低采样频率下的滤波器约束很难处理。过采样以高于奈奎斯特频率极限的速率对模拟输入信号进行采样,对样本进行过滤,并通过抽取来降低采样率。使用该方法以实现抗混叠低通滤波器弛豫。
在大多数情况下,认为量化噪声和输入信号是无关的。在这种情况下近似为高斯噪声,并且在奈奎斯特带宽上或多或少的波动。
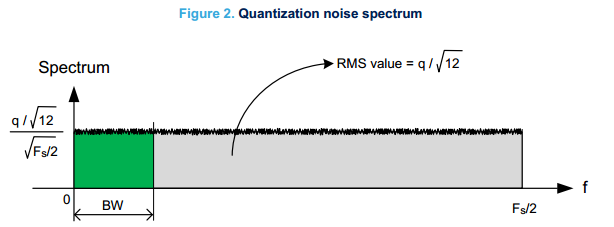
在采样时钟和信号谐波相关的特定条件下,量化噪声会与输入信号相关。它的能量主要集中在信号的谐波中,在量化噪声不表现为随机噪声的情况下,必须要使用Dithering。
通常输入信号带宽小于 \frac{F_s}{2},如果使用数字滤波器除去带宽以外的噪声(该滤波器比抗混叠滤波器更精确),则总RMS噪声降低,量化噪声的均方根除以一个比值,该比值取决于输入信号带宽和采样频率。
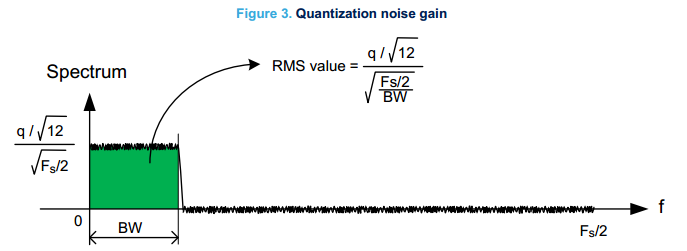
通过过滤带宽外的噪声,将增益考虑在内,重新表述信噪比:
其中OSR为过采样率:
上述的两种情况,第一种情况下量化噪声不是随机的,第二中种情况在输入信号小于量化步长的时候,理论上没有发生转换。可以使用抖动技术解决这些问题,即在输入信号加一个小的高斯噪声,获得一个可以确保LSB切换的信号,噪声还确保量化噪声始终是随机的,独立于输入信号。
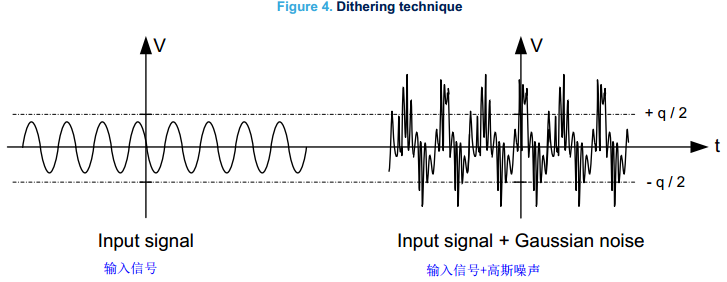
如果对噪声进行塑造,可以大大降低信噪比的影响。


评论区